I tried to record a video to show the solution but my recording gear is terrible. I'll search for a good microphone.
From the exercise we can extract all the important variables.
Follow:
- Rotor Lobes : 7
- Rotor Length : 5.8 m
- MAX OD : 6.5 in
- MIN OD : 5 in
- Pitch : 1.45 m/rev
One thing we might have to infer while drawing the rotor is the lobe offset. I will show you while performing the drawing.
To make our lives easier we will use all the above values at the end. I'll show you how to fix everything when we finished with the drawing.
- Rotor Lobes : 7
- Rotor Length : 2*
- MAX OD : 14 m
- MIN OD : 12 m
- Pitch : 2*
m/rev
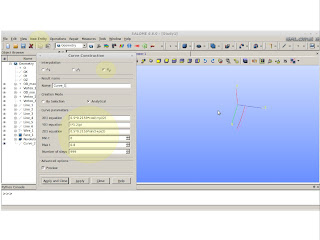
First, we know that hypocycloid is a set of parametric equations and can be taken at http://en.wikipedia.org/wiki/Hypocycloid.
On the following picture you will observe I put the set of parametric equations and the rest of the values. We don't want a whole hypocycloid. We want only a piece of it and from this piece we can provide the rest. For "Min t" I'm using 0.15 /rad because if I put zero I'm going to have a spike (and we don't need that). "Max t" is going to be divided by the quantity of lobes. In this case, ~0.448799.
/rad because if I put zero I'm going to have a spike (and we don't need that). "Max t" is going to be divided by the quantity of lobes. In this case, ~0.448799. |
| New Entity >> Basic >> Curve |
Right know comes the "engineering" assumption. A Moineau pump, of course, doesn't have all those cuspids and we need to round them up. To create the lobes we must have a rolling small inner circle inside of a big one. For this case the big circle has a 7 m radius and to have a seven lobes we must have the a small circle with 1 m radius. So ... we need to create an "insider" tangent circle.
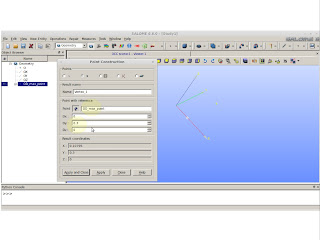
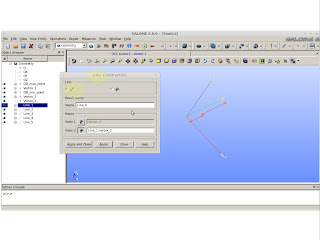
Create the point:
 |
| New Entity >> Basic >> Point |
Create the circle based on the last point:
 |
| New Entity >> Basic >> Circle |
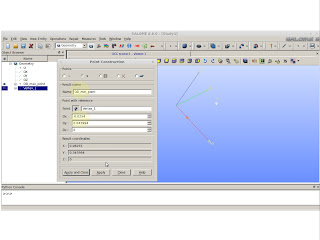
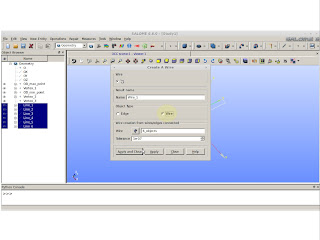
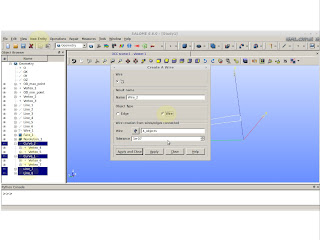
Build a wire:
 |
| New Entity >> Build >> Wire |
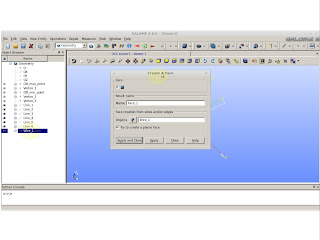
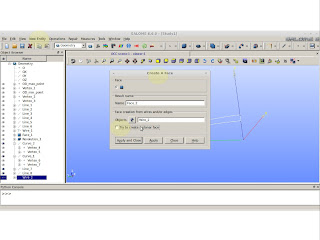
Build an edge (you do want to do this because we can extract some values from this edged curve):
 |
| New Entity >> Build >> Edge |
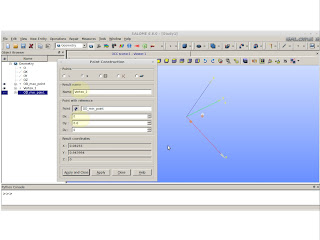
By now, we should observe the hypocycloid curve is intersecting the small circle. That is when we have the offset. We want this curve to be as much tangent as possible. I'm using an offset of 1.17 ... it is going to give you a nice tangent figure.
 |
| Operations >> Transformation >> Scale Transform |
Fuse the results from the scaled up hypocycloid curve and the small circle.
 |
| Operations >> Boolean >> Fuse |
You must be asking yourself "What are you doing?!!". But this is the idea, to make your life easy. If you have symmetry in your subject you must use it in your favor, otherwise, you would be wasting time.
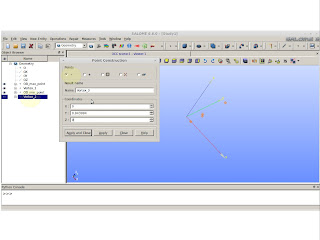
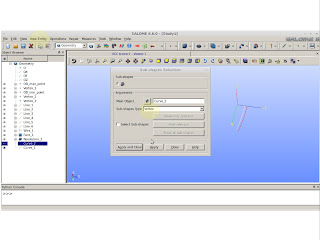
We must clean the resultant fuse. Explode the edges and create a curve for only what we need to have. Remember, we are aiming on a lobe design.
 |
| New Entity >> Explode |
Choose which edges we need:
In my case I'm going to need edges 3,5 and 6.
Create a wire from the chosen edges:
 |
| New Entity >> Build >> Wire |
Mirror the resultant curve and fuse both curves. We can see something close to a lobe.
 |
| Operations >> Transformation >> Mirror Image |
Explode it into vertexes.
 |
| New Entity >> Explode |
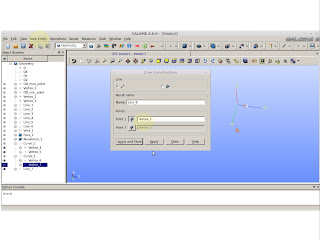
In my case, I will need the beginning and the of the curves. Vertex 2 and Vertex 3. By having these two vertexes we can create a reverse arc.
 |
| New Entity >> Basic >> Arc |
We can see a wire from a lobe. We are almost there. Just create a a wire with this arc and the connected curve.
 |
| New Entity >> Build >> Wire |
Build a face:
 |
| New Entity >> Build >> Face |
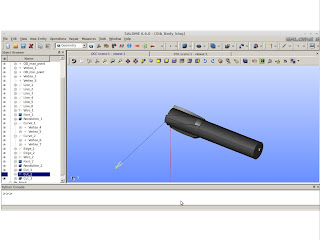
Do you remember that I stated in a Moineau pump the axial section would look like a helix? We need to make two helical curves. One curve is going to give me the helical path and the other curve is going to give the binormal vector. Without this binormal vector the lobe would get flat while rounding up. We don't want that!!!
First curve must have a radius of 6 m (small circle's center) and the second, 7 m (hypocycloid radius). We want only a full circle that is why we must have 2 at "Max t".
at "Max t".
Build the first curve and I will let you build the second:
 |
| New Entity >> Basic >> Curve |
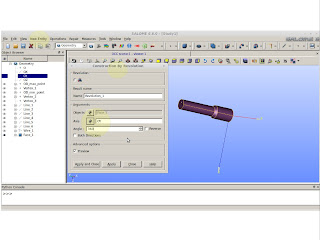
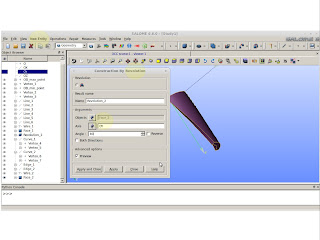
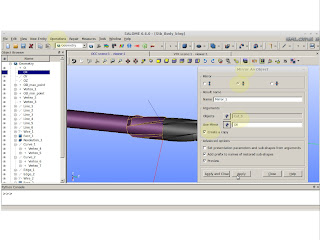
Create an extrusion along a path. Remember we will use a binormal!!
 |
| New Entity >> Generation >> Extrusion Along a Path |
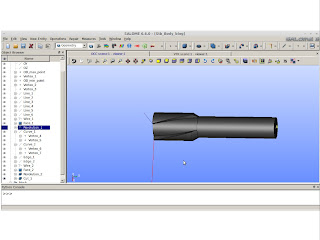
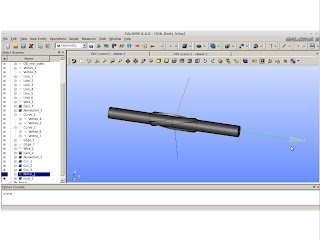
We have one lobe! Time to make 6 more.
Perform a multi-rotation:
 |
| Operations >> Transformation >> Multi-Rotation |
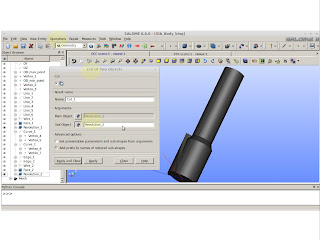
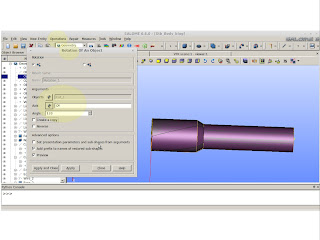
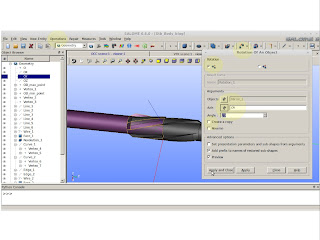
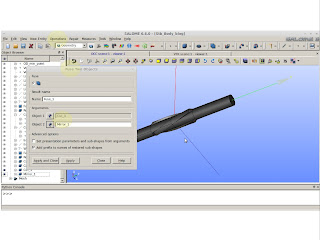
We have a nice screw. Time to put everything in corrected values. To do this we need to scale down every axis by the corrected amount. It takes into account unit and size conversion only.
 |
| Operations >> Transformation >> Scale Transform |
1.45 m Moineau Rotor , if you want the complete 5.8 m just translate a copy and fuse them.
 |
| Answer |
Any doubt, just ask.
Cheers!!!!
