Jet Nozzle Flow and CFD Simulation

2 Jet Nozzle Flow

2.1 Hydraulic Impact Force

In the drilling industry we usually assume that the jet will impact the hole bottom without loss of momentum [7] and, sometimes, can be wrongly interpreted (mainly when we have a big clearance between the bit attack area and the bottom of the well) as having the same velocity profile hitting the bottom. Lets us take the most used formula to calculate the hydraulic impact force in pounds:

(1) F_j = 0.01823C_dq√(ρΔp_b)

Where C_dis a discharge coefficient that ranges between 0.95 and 1.03; q is the flow rate in gpm; ρ, the fluid density in pounds per gallon and Δp_bis pressure drop across the bit in psi. Having this in mind and taking into consideration an usual drilling parameters regarding hydraulics we have the following:

TFA	Cd	q	ρ	Δpb	Fj
0.969 in²	0.95	600 gpm	9.6 ppg	338.9 psi	592.7 lbf
625.16 mm²	0.95	2271.25 lpm	1.15 g/cm³	2.3366 MPa	2636.46 N

Proceeding with a simple math, following the assumption that the jet won’t spread out before hitting the bottom and every jet (doesn’t matter its diameter) will keep the same impinging velocity, we have a hydraulic impact pressure value of 611 psi ( 4.2127 MPa ) for each nozzle.

2.2 Spreading Out the Jet and Cavitating Clouds

It is going to be seen that the flow of submerged jets are well known [8] and posses some distinct regions (4↓):

Figure 4 The flow regions of an impinging jet (adapted from Zuckerman)[8].

From (4↑) is possible to see that when the jet exits the nozzle, the velocity gradient creates shearing at the edges which transfers momentum. Taking into account this process we can easily visualize the jet dissipates energy and the velocity profile is widened.

Sato et al [9] carried out experiments where they had a submerged jet nozzle and they used these experiments to investigate the occurrence of cavitating clouds where they saw a ring-like erosion distribution over an acrylic plate that could be related to cavitation on impinging walls. Hutli [10]concluded through experiments that the cavitation exhibits a regular frequency of oscillation. It is known that cavitation in a well can occur on very shallow depths, but when we are deep is quite difficult its appearance. The key behind bringing this subject is the already mentioned statement "cavitation exhibits a regular frequency of oscillation", so, if cavitation happens on submerged nozzles in above mentioned experiments, the occurrence of low pressure zones in deep wells are possible and they are cyclic.

3 CFD Simulation

Having this background, and in order to capture these low pressure zones, were simulated the same boundary geometry (5↓) and three different nozzle diameters having a high density of nodes at the shear layer: 10/32" (7↓), 12/32" (8↓) and 14/32" (9↓) with 60 m/s (196.85 ft/s) of jet velocity with the same drilling fluid parameters ( MW= 9.6 ppg, YP= 27 cP, PV=22cP). The difference of hidrostactic pressure between the inlet of the nozzle and the bottom of the hole is negligible when compared with the impinging pressure.

The simulation was carried out using Openfoam on a Debian based computer with a transient PISO algorithm. Each run took 24 hours to be solved.

Figure 5 Simulation’s geometry.

Figure 6 20 degrees wedge simulation’s axisymmetric mesh. The flow is towards z-axis positive direction and the nozzle’s center is located at the origin .

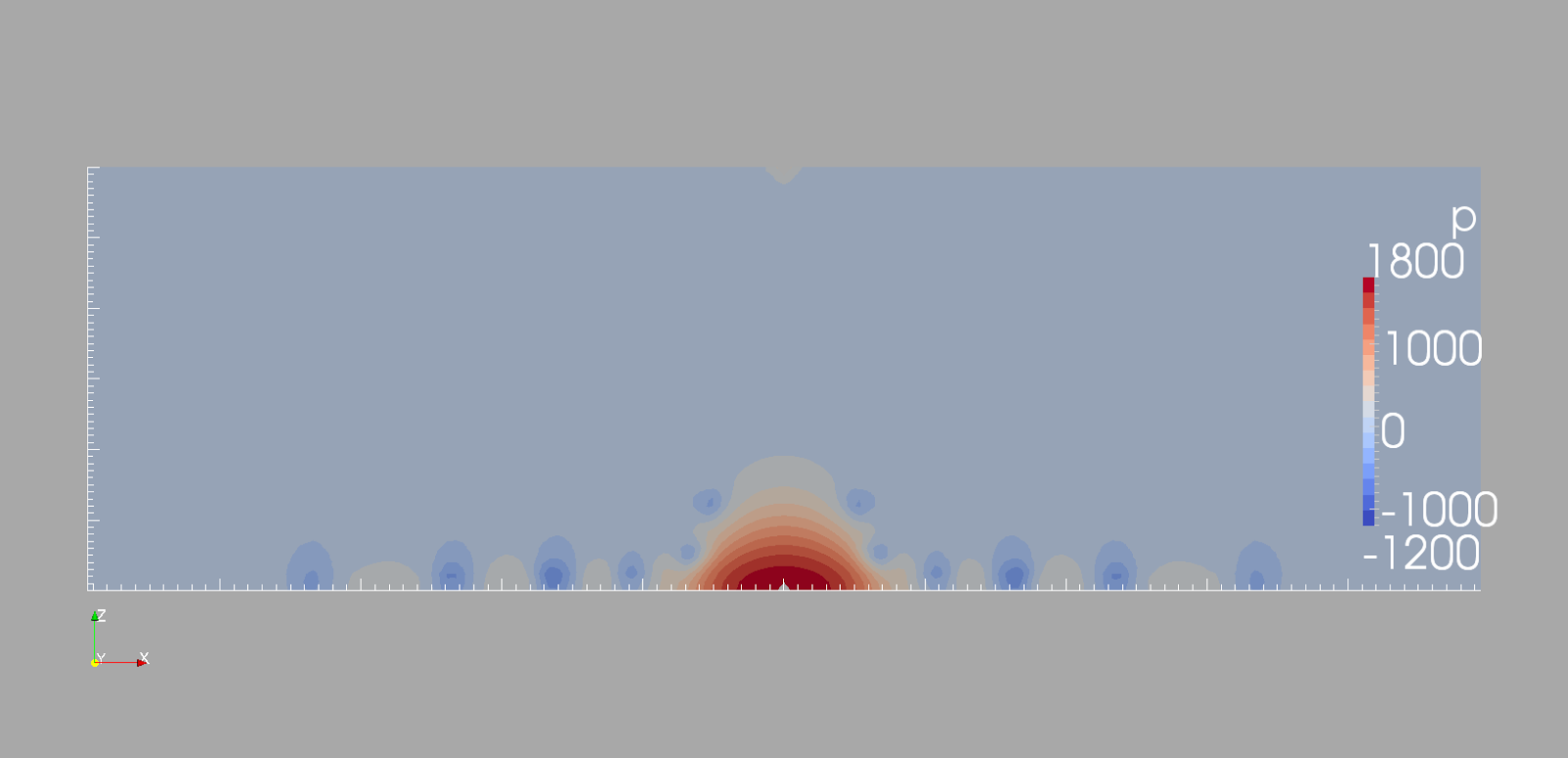
We can see that the jet velocity (7↓,8↓,9↓), just before hitting the bottom of the well, is no longer the same as the nozzle exit and just at the impingement area we can see a stagnation region.

Figure 7 Velocity profile for 10/32" Nozzle with average exit velocity of 60 m/s (196.85 ft/s) after reaching fully developed flow.

Figure 8 Velocity profile for 12/32" Nozzle with average exit velocity of 60 m/s (196.85 ft/s) after reaching fully developed flow.

Figure 9 Velocity profile for 14/32" Nozzle with average exit velocity of 60 m/s (196.85 ft/s) after reaching fully developed flow.

The simulations regarding the pressure profiles gave us some very good results. The PISO algorithm uses the kinematic viscosity to solve the Navier Stokes equations, so, the results are the rho-normalized pressure with units in (m²/s²). For the case of this used drilling fluid we should expect values close to 2031 m²/s². We can see in ( 10↓, 11↓, 12↓ ) that the values are quite close to the expected value. In fact they are smaller, this is because in the F_j equation is not assumed we have energy losses between the jet and the surrounding fluid.

Figure 10 Pressure profile for 10/32" Nozzle. Maximum pressure of 1719 m²/s² (517 psi) and Minimum pressure of -510 m²/s² (-153 psi).

Figure 11 Pressure profile for 12/32" Nozzle. Maximum pressure of 1813 m²/s² (545 psi) and Minimum pressure of -606 m²/s² (-182 psi).

Figure 12 Pressure profile for 14/32" Nozzle. Maximum pressure of 1860 m²/s² (560 psi) and Minimum pressure of -1161 m²/s² (-349 psi).

References

[1] Carlos H.L. Bruhn, José Adilson T. Gomes, Cesar Del Lucchese Jr., and Paulo R.S Johann – “Campos Basin: Reservoir Characterization and Management – Historical Overview and Future Challenges”, OTC 15220, 2003.

[2] Bernardo, R.J, Saliés, J.B., and Polilo Filho, A.: “Campos Basin: Lessons Learned and Critical Issues to be Overcome in Drilling and Completion Operations”, OTC 15221, 2003.

[3] B. S. McLaury, S. A. Shirazi, Q. H. Mazumder, V. Viswanathan – “Effect of Upstream Pipe Orientation on Erosion in Bends for Annular Flow”

[4] Bill Chemerinski, SPE , Imperial Oil Resources, Ltd. and Leon Robinson, SPE, OGCI – “Hydraulic Wellbore Erosion While Drilling”

[5] Zeidler. H. Udo, Oyez Business Seminar, Innovations in Bit Technology, Oct. 9.1981, Houston. Texas – “Hydraulics and Hole Erosion”

[6] Steve Barton, Kirk Card, and Garrett Pierce, NOV Downhole – “Delivering Steering Success in Problematic Soft Formation Directional Wells”

[7] A. T. Burgoyne Jr., K. K. Milheim, M. E. Chevernet, F.S. Young Jr. - "Applied Drilling Engineering"

[8] N. Zuckerman and N. Lior - "Jet Impingement Heat Transfer: Physics, Correlations, and Numerical Modeling"

[9] K. Sato, Y. Sugimoto and S.Ohjimi - "Pressure-Wave Formation and Collapses of Cavitation Clouds Impinging on Solid Wall in a Submerged Water Jet"

[10] E. A. F. Hutli and M. S. Nedeljkovic - "Investigation of a Submerged Cavitating Jet Behavior: Part One - The Phenomenon, Detection Technique and Sono-Luminescence"